[ Contents ]
1. 동적 프로그래밍(Dynamic Programming, 동적계획법)

동적계획법(Dynamic programming, DP): 작은 문제들에 대한 결과를 배열(리스트)에 저장하고, 이를 이용해서 입력 크기가 더 큰 문제를 점진적으로 해결하는 방법
동적계획법은 이전 문제들의 답을 메모해두는 알고리즘입니다. 메모해두면, 동일한 문제가 나왔을 때 바로 답을 찾아서 쓸 수 있습니다. 다시 계산할 필요가 없기 때문에, 이전 문제의 해가 필요할 때 많은 시간을 절약할 수 있습니다.
fibo(0) = 0
fibo(1) = 1
fibo(2) = fibo(1) + fibo(0)
fibo(3) = fibo(2) + fibo(1)
...
fibo(n) = fibo(n-1) + fibo(n-2)
다이나믹 프로그래밍은 '피보나치 수열'과 같이, 이전에 계산한 문제의 해가 반복해서 필요할 때 유용합니다. 만약 전에 계산한 피보나치 값을 저장해 두지 않는다면, 매번 다시 계산해야 합니다.
2. 메모이제이션(Memoization)
메모이제이션: 이전에 계산한 값을 메모리에 저장하고, 동일한 계산이 나왔을 때 불러와서 사용하는 기법
한국어 음역이 조금 독특합니다. 메모리제이션이 아니라 메모'이'제이션입니다. 메모이제이션은 '캐싱'과 같이 메모리에 저장하고 불러와서 쓰는 기법입니다. 동적 계획법의 핵심 기법으로, 배열이나 리스트에 결괏값을 저장하고 불러와서 사용합니다.
def calFibonacci(n):
cache = [0, 1] #fibo(0) = 0, fibo(1) = 1
for i in range(2, n+1):
cache.append(cache[i-1] + cache[i-2])
return cache위 코드는 피보나치수열을 '동적계획법'으로 구현한 알고리즘입니다. 피보나치수열은 이전 계산값을 반복해서 사용해야 합니다. ( fibonacci(n) = fibonacci(n-1) + fibonacci(n-2) )
메모이제이션 기법을 이용하면, 0~n까지의 피보나치 계산값을 저장해 두고 불러와서 사용할 수 있습니다. cache가 메모리 역할을 해주며, 이미 계산한 값이 있을 경우(초기화 값인 -1이 아닐 경우) 그대로 불러와서 사용합니다.
3. 동적 계획법 적용 단계
1. 최적성의 원리가 성립하는지 확인
작은(부분) 문제들의 최적해를 통해 주어진 문제의 최적해를 구할 수 있으면, '최적해의 원리'가 성립합니다. 그리디 알고리즘과 달리, 동적 계획법은 작은 문제들의 해를 조합해서 모든 가능성을 고려할 수 있습니다. 따라서, 항상 최적해를 보장합니다.
2022.01.26 - [Algorithm] - [Algorithm] 탐욕적인 그리디 알고리즘, 직관적이고 쉬운 문제해결
[Algorithm] 탐욕적인 그리디 알고리즘, 직관적이고 쉬운 문제해결
경주마들을 자세히 보면, 양쪽 시야를 차단하는 안대를 끼고 있습니다. 이를 '차안대' 라고 합니다. 말의 눈은 양 옆에 달려 있어 시야가 '350도'나 됩니다. 자기 자신 빼곤 다 보이기 때문에, 다
star7sss.tistory.com
(그리디 알고리즘은 현 단계의 상황만 고려)
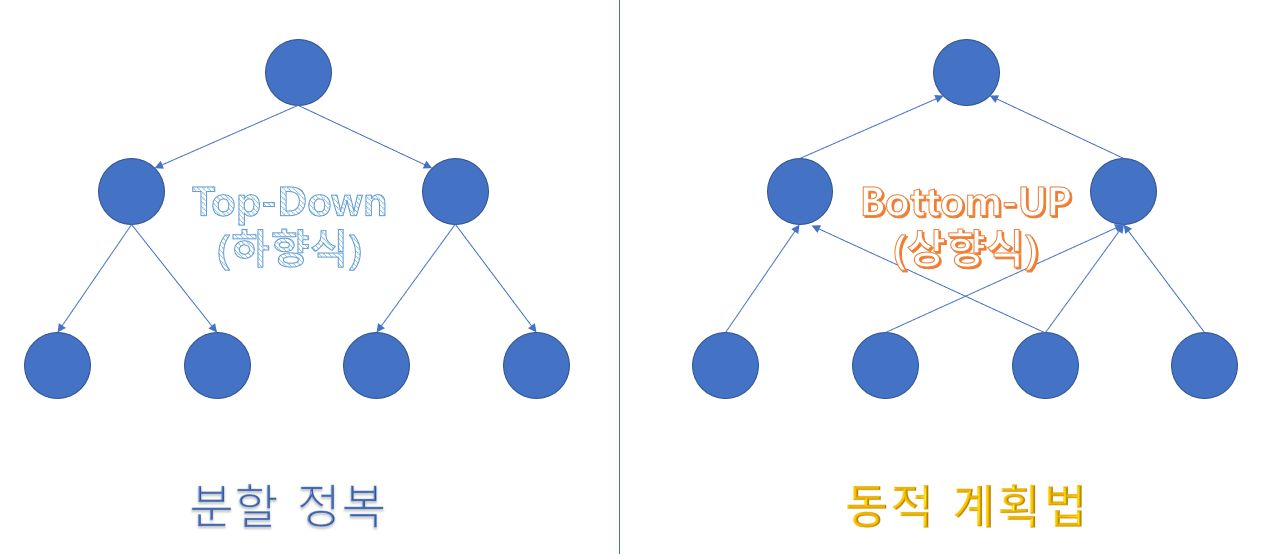
분할정복 알고리즘과 비교하면, 동적 계획법은 부분 문제의 해를 자유롭게 여러 번 사용할 수 있습니다. 반면 분할정복 알고리즘은 분할된 문제의 해를 조합해서 큰 문제의 해를 얻습니다. 분할된 문제의 해는 분할했던 큰 문제의 해를 얻기위해 1번 사용됩니다.
만약 분할 정복 알고리즘에서, 동일한 부분 문제들이 자주 나타나면 매번 새로 계산해야 하는 비효율성이 생깁니다. 이 때는 분할정복이 아니라 '동적 계획법'으로 풀이해야 합니다.
2022.01.29 - [Algorithm] - [Algorithm] 분할정복(DQ, Divide-and-Conquer), 각개격파 알고리즘
[Algorithm] 분할정복(DQ, Divide-and-Conquer), 각개격파 알고리즘
각개격파(各個擊破): 적을 하나하나 따로 떼어 무찌름 유독 외세의 침략을 많이 받았던 우리 민족의 대표적인 전술은 '매복'과 '각개격파'였습니다. 70%가 산악지형인 점을 이용해서, 산개된 적
star7sss.tistory.com
(분할정복 알고리즘 관련 설명글)
2. 최적해를 구하는 점화 관계식 도출
수열의 점화식과 비슷합니다. 작은 문제들의 해로부터 큰 문제의 해를 구할 수 있는 점화 관계식을 도출해야 합니다. 예를 들어, 피보나치 수열의 경우는 fibonacci[n] = fibonacci[n-1] + fibonacci[n-2] 입니다.
3. 가장 작은 부분 문제의 해부터 테이블에 저장
피보나치 수열의 경우, n=0과 n=1인 해를 저장해둡니다. 그래야 점화 관계식을 통해서 fibonacci[2] = fibonacci[1] + fibonacci[0]을 구할 수 있습니다. 이때 구한 fibonacci[2]도 테이블에 저장되며, fibonacci[3]을 구하는 데에 이용됩니다.
4. 테이블에 저장된 부분 문제의 해로부터 점차 입력 크기가 큰 문제의 해를 구해나감
저장된 부분 문제들의 최적해로부터 주어진 문제의 최적해를 도출합니다.
<전체 과정>
1. 최적성의 원리가 성립하는지 확인
2. 최적해를 구하는 점화 관계식 도출
3. 가장 작은 부분 문제의 해부터 테이블에 저장
4. 테이블에 저장된 부분 문제의 해로부터 점차 입력 크기가 큰 문제의 해를 구해나감

'Algorithm' 카테고리의 다른 글
| [DP/동적계획법] 백준 2748 피보나치 수 2 - Python (0) | 2022.02.13 |
|---|---|
| [DP/동적계획법] 백준 1003 피보나치 함수 - Python (0) | 2022.02.13 |
| [자료구조/해시] 백준 1620 나는야 포켓몬 마스터 이다솜 - Python (0) | 2022.02.12 |
| [구현/비트마스킹] 백준 11723 집합 - Python (0) | 2022.02.11 |
| [자료구조/해시] 백준 15829 Hashing - Python (0) | 2022.02.11 |




댓글