
[ Contents ]
1. 문제 (링크 참조)
1074번: Z
한수는 크기가 2N × 2N인 2차원 배열을 Z모양으로 탐색하려고 한다. 예를 들어, 2×2배열을 왼쪽 위칸, 오른쪽 위칸, 왼쪽 아래칸, 오른쪽 아래칸 순서대로 방문하면 Z모양이다. N > 1인 경우, 배열을
www.acmicpc.net
2. 문제 풀이
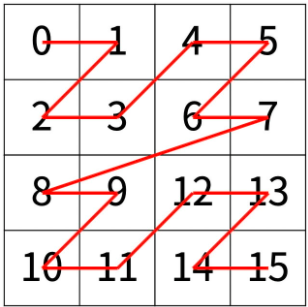
위와 같이 Z 모양으로 이동하는 규칙이 있습니다. 이 때, 2^N * 2^N크기의 r행 c열의 순서를 구하는 문제입니다.
2022.01.29 - [Algorithm] - [Algorithm] 분할정복(DQ, Divide-and-Conquer), 각개격파 알고리즘
[Algorithm] 분할정복(DQ, Divide-and-Conquer), 각개격파 알고리즘
각개격파(各個擊破): 적을 하나하나 따로 떼어 무찌름 유독 외세의 침략을 많이 받았던 우리 민족의 대표적인 전술은 '매복'과 '각개격파'였습니다. 70%가 산악지형인 점을 이용해서, 산개된 적
star7sss.tistory.com
4분할로 나누는 분할정복 문제입니다. 다만, 시간 제한이 0.5초로 짧습니다. 단순히 재귀함수를 이용한 분할정복으로 짜면 시간 초과가 납니다.
3. 코드
N, r, c = map(int, input().split()) #2^N * 2^N 중 r행 c열
num = 0
#분할 정복
def z(n, i, j):
# 2*2크기이면 Z
if n == 1:
global num
for x, y in [(i,j), (i, j+1), (i+1, j), (i+1, j+1)]:
if x == r and y == c:
print(num)
num += 1
# 4분할
else:
z(n-1, i, j)
z(n - 1, i, j + 2 ** (n - 1))
z(n-1, i+2**(n-1), j)
z(n-1, i+2**(n-1), j+2**(n-1))
z(N, 0, 0)원래 4분할로 나눠서 재귀로 호출하는 방법을 썼습니다. 작동은 문제 없으나, 시간초과가 납니다.
N, r, c = map(int, input().split()) #2^N * 2^N 중 r행 c열
num = 0
#분할 정복
while N != 0:
N -= 1
# 1사분면
if r < 2**N and c < 2**N:
num += 0
# 2사분면
elif r < 2**N and c >= 2**N:
num += (2**N) * (2**N)*1
c -= 2**N
# 3사분면
elif r >= 2**N and c < 2**N:
num += (2**N) * (2**N)*2
r -= 2**N
# 4사분면
else:
num += (2**N) * (2**N)*3
r -= 2**N
c -= 2**N
print(num)재귀 없이, N을 1씩 내려가며 어느 4분면에 해당하는지 찾습니다. 해당하는 4분면의 좌측 최상단 좌표로 원점(0,0)을 맞추고, 번호도 세줍니다.

'Algorithm' 카테고리의 다른 글
| [구현/수학] 백준 11282 한글 - Python (0) | 2022.02.25 |
|---|---|
| [구현/수학] 백준 11283 한글 2 - Python (0) | 2022.02.25 |
| [탐색/BFS] 백준 7576 토마토 - Python (0) | 2022.02.24 |
| [탐색/BFS] 백준 1697 숨바꼭질 - Python (0) | 2022.02.24 |
| [탐색/BFS] 백준 1012 유기농 배추 - Python (0) | 2022.02.23 |




댓글