모든 쌍의 최단 경로를 '플로이드 - 와샬' 알고리즘으로 구하는 방법을 알아보고, 구현 코드도 살펴보겠습니다.
[ Contents ]
1. 모든 쌍의 최단 경로
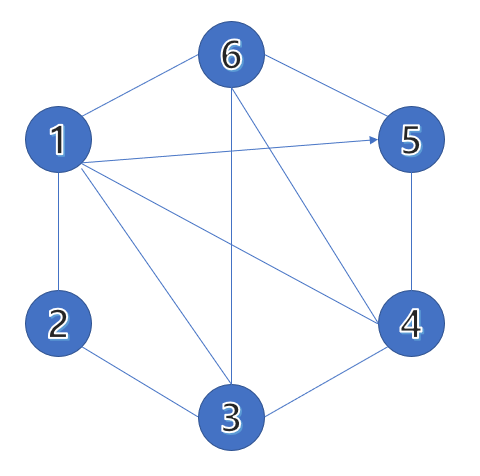
위 그래프 그림에서 '노드(Node)'는 원으로 된 지역이고, '간선(Edge)'은 각 지역으로 이동할 수 있는 경로입니다. 간선마다 이동거리 혹은 이동시간에 따른 가중치가 부여됩니다.
'모든 쌍의 최단 경로'는 말 그대로, 지역 간 최단거리를 구하는 작업입니다. 보통은 A에서 B로 바로 가면 빠르지만, 경유지를 거쳐서 가는 게 더 지름길일 때도 있죠. 이런 경우를 모두 고려해서 계산해야 합니다.

예를 들어, 위 경로에서는 1->3으로 바로 가는 것보다, 2를 경유해서 가는 게 더 빠릅니다.
2. 플로이드 - 와샬(Floyd-Warshall) 알고리즘
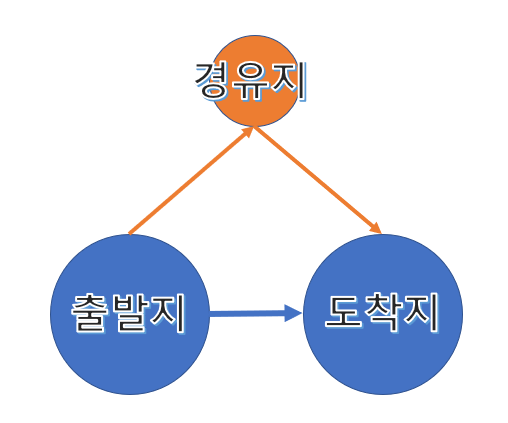
플로이드 - 와샬 알고리즘: 모든 경유지를 고려해서 최단 거리를 구하는 알고리즘
플로이드 - 와샬 알고리즘은 '경유지를 거치는 경로(경유)'와 '곧장 가는 경로(직통)'를 비교해서 최단 경로를 찾아냅니다. 모든 경유지를 고려해서 비교하며, 이 때 경유지를 거치는 경로 역시 최단 경로여야 합니다.
2022.02.12 - [Algorithm] - [Algorithm] 메모해두고 불러와서 사용하는 동적 프로그래밍(DP)
[Algorithm] 메모해두고 불러와서 사용하는 동적 프로그래밍(DP)
[ Contents ] 1. 동적 프로그래밍(Dynamic Programming, 동적계획법) 동적계획법(Dynamic programming, DP): 작은 문제들에 대한 결과를 배열(리스트)에 저장하고, 이를 이용해서 입력 크기가 더 큰 문제를 점진..
star7sss.tistory.com
경유지를 거치는 최단 경로는 이전에 계산해둔 값을 불러와서 사용합니다. 따라서 플로이드-와샬 알고리즘은 DP(다이나믹 프로그래밍, 동적계획법)을 포함하고 있습니다.
3. 구현 코드
#플로이드 와샬 알고리즘
def floyd(n, dist):
# 최단 경로 리스트 초기화
for via in range(n): #경유지
for start in range(n): #출발지
for end in range(n): #도착지
# 경유해서 가는 게 더 빠르다면, 최단거리를 갱신
if dist[start][end] > dist[start][via] + dist[via][end]:
dist[start][end] = dist[start][via] + dist[via][end]
return dist단순히 '경유지를 거치는 비용'과 '곧장 가는 비용'만을 비교하는 쉬운 알고리즘입니다. 3중 for문을 쓰기 때문에 시간복잡도는 O(n^3)이지만, 로직이 간단해서 효율적이라고 알려져 있습니다. (다익스트라 알고리즘과 시간복잡도는 동일하지만, 계산이 훨씬 간단합니다.)

위 그래프를 예시로 플로이드-와샬 알고리즘을 적용해보겠습니다.
#플로이드 와샬 알고리즘
def floyd(n, dist):
# 최단 경로 리스트 초기화
for via in range(n): #경유지
for start in range(n): #출발지
for end in range(n): #도착지
# 경유해서 가는 게 더 빠르다면, 최단거리를 갱신
if dist[start][end] > dist[start][via] + dist[via][end]:
dist[start][end] = dist[start][via] + dist[via][end]
return dist
#노드 간 가중치 (경로가 없으면 10000으로 표현)
graph = [[0, 1, 3, 2], [1, 0, 1, 2], [3, 1, 0, 10000], [2, 2, 10000, 0]]
dist = floyd(4, graph)
#결과 출력
for i in dist:
print(i)

위 그래프와 비교해보면 결과도 잘 나온 걸 확인할 수 있습니다.

'Algorithm' 카테고리의 다른 글
| [탐색/플로이드] 백준 1389 케빈 베이컨의 6단계 법칙 - Python (0) | 2022.02.28 |
|---|---|
| [탐색/플로이드] 백준 11403 경로 찾기 - Python (0) | 2022.02.28 |
| [그리디/수학] 백준 10610번 30 - Python (0) | 2022.02.28 |
| [구현/수학] 백준 15080 Every Second Counts - Python (0) | 2022.02.28 |
| [구현/수학] 백준 15726 이칙연산 - Python (0) | 2022.02.27 |




댓글