그래프의 트리 구조 중 하나인 '힙'과 구현 방법에 대해 알아보고, 그와 관련된 우선순위 큐도 살펴보겠습니다.
[ Contents ]
1. 완전 이진트리(Complete Binary Tree)

완전 이진트리: 왼쪽부터 오른쪽으로 한 줄씩 채워가는 이진트리
트리(Tree) 구조는 마치 나무의 뿌리가 뻗어나가는 것처럼 위에서 아래로 확장되는 그래프 구조를 갖고 있습니다. 그래프에서 데이터는 '노드(node)'에 담기며, 맨 위 노드를 '루트(Rout) 노드'라고 합니다.
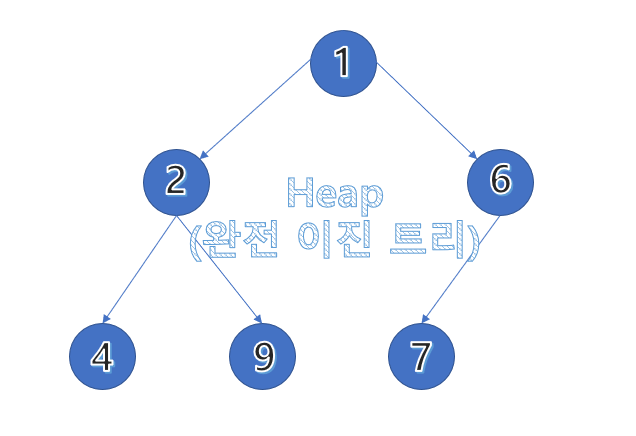
자신의 아래층에 있는 노드는 '자식 노드'이고, 위층에 있는 노드는 '부모 노드'입니다. 루트 노드는 부모 노드가 없으며, 리프(leaf) 노드는 자식 노드가 없습니다. (위 그래프에서 루트 노드: 1 / 리프 노드: 4, 9, 7)
이진트리(Binary Tree)는 자식 노드가 최대 2개인 트리를 말합니다. 그 중 완전 이진트리는 왼쪽부터 오른쪽으로 한 줄씩 채워나가는 그래프입니다.

위와 같이, 새로운 데이터가 들어오면 왼쪽부터 오른쪽으로 한 줄씩 채워갑니다. 다만, Heap은 자식 노드가 반드시 부모 노드보다 커야 합니다. (위에서부터 아래로 오름차순 정렬)
만약 자식 노드가 더 작다면, 부모 노드와 자리를 바꿔줍니다.

이런 식으로 최솟값이 '루트 노드'가 되도록 완전 이진 트리를 유지합니다.
2. 힙(Heap)과 우선순위 큐(Priority Queue)
Heap: 완전이진트리를 이용하여 최댓값 및 최솟값으로 정렬하는 자료구조
위에서 말했듯이, Heap는 부모 노드가 자식 노드보다 작게 만들어서 위에서부터 아래로 오름차순 정렬합니다. 항상 최솟값은 '루트 노드'이며, 루트 노드에서만 pop 하면 자연스럽게 오름차순된 결과를 얻을 수 있습니다.
이게 바로, 우선순위 큐입니다. 데이터를 추가(push)할 때에는 자유롭게 할 수 있지만, 데이터를 꺼낼 때에는 최솟값부터 추출(pop)합니다.

heap구조에서 최솟값을 추출(pop)하고 복구하는 과정을 알아보겠습니다. heap 구조에서는 루트 노드가 비면, 우측 하단의 노드로 채웁니다.
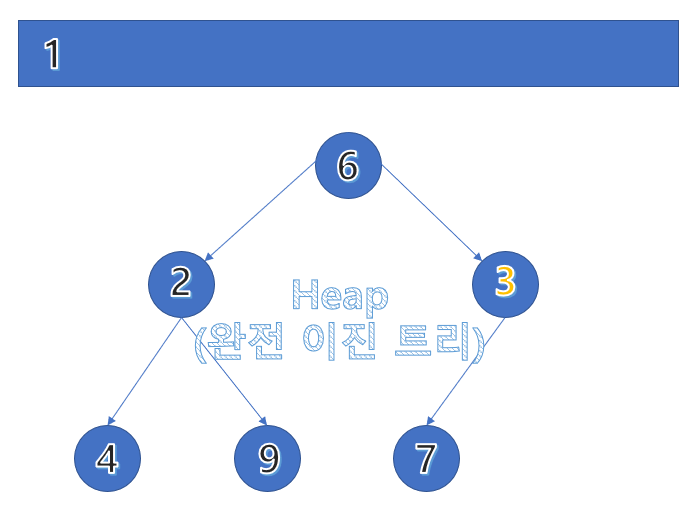
6을 루트 노드로 올린 뒤, 부모 노드와 자식 노드의 관계를 재정립합니다. 부모 노드가 자식 노드보다 더 큰 경우에는, 자식 노드 중 더 작은 쪽과 교환합니다.

마찬가지로, 4가 6보다 작으므로 둘의 자리를 교환합니다.

총 두 번의 교환 끝에 완료되었습니다. 최솟값을 추출(push)할 때마다 0회 ~ 트리 높이(층)만큼 연산합니다.
3. 힙 구현
import heapq
heap = [] #리스트로 생성
heapq.heappush(heap, 1) #push
heapq.heappop(heap) #pop파이썬에서 heap은 heapq 라이브러리를 이용합니다. 일반 리스트로 우선순위 큐를 구현하며, heappush와 heappop 함수로 추가하고 추출합니다.
| heapq.heappush(heap, x) | heap에 x를 추가 |
| heapq.heappop(heap) | heap에서 최솟값을 제거한 뒤 반환 |
| heap[0] | heap의 최솟값을 반환 |
| not heap | 비어있으면 True(1), 아니면 False(0) 반환 |

'Algorithm' 카테고리의 다른 글
| [자료구조/힙] 백준 11279 최대 힙 - Python (0) | 2022.02.20 |
|---|---|
| [자료구조/힙] 백준 1927 최소 힙 - Python (0) | 2022.02.20 |
| [구현/수학] 백준 14470 전자레인지 - Python (0) | 2022.02.19 |
| [구현/수학] 백준 14264 정육각형과 삼각형 - Python (0) | 2022.02.19 |
| [구현/수학] 백준 17388 와글와글 숭고한 - Python (0) | 2022.02.19 |




댓글