다익스트라는 출발지부터 목적지까지의 최적 경로를 탐색해주는 알고리즘입니다. 다익스트라의 이론적 설명과 구현 방법, 경로 추적까지 살펴보겠습니다.
[ Contents ]
1. 다익스트라(Dijkstra) 알고리즘
다익스트라(Dijkstra): 현재까지 찾은 최적경로를 바탕으로 목적지까지의 최단경로를 탐색하는 알고리즘
출발지에서 가까운 지점부터 차례대로 최단경로를 탐색하며, 목적지까지의 최단경로를 탐색하는 알고리즘입니다. 그리디 알고리즘 기법으로, 한 번 결정된 최단 경로는 절대 바뀌지 않으며 이를 바탕으로 목적지까지의 최단경로를 계산합니다.
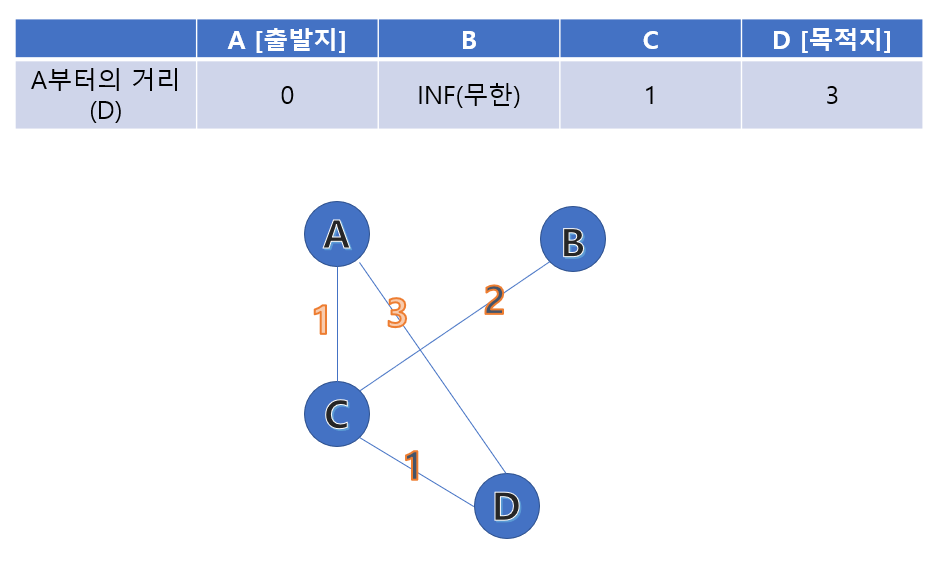
예를 들어, 출발지 A에서 목적지 D까지의 최단경로를 구해봅시다. 다익스트라 알고리즘에서는 A 주변 노드부터 최단거리를 계산하고, 점차 넓혀갑니다.
아직 A와의 거리를 모르면, Infinite(무한)으로 초기화하고 진행합니다.

이전 단계에서 알게 된 노드(C, D)와 연결된 노드까지의 거리를 계산합니다. C까지의 최단거리는 1로 결정되었고, C에서 D로 가는 최단 거리는 1입니다. 따라서 A에서 D까지의 최단거리가 2로 갱신됩니다.
2. 구현 코드
import heapq # 우선순위 큐 구현을 위함
def dijkstra(graph, start):
distances = {node: int(1e9) for node in graph} # 처음 초기값은 무한대
distances[start] = 0 # 시작 노드까지의 거리는 0
queue = []
heapq.heappush(queue, [distances[start], start]) # 시작 노드부터 탐색 시작
while queue: # queue에 남아있는 노드가 없을 때까지 탐색
dist, node = heapq.heappop(queue) # 탐색할 노드, 거리
# 기존 최단거리보다 멀다면 무시
if distances[node] < dist:
continue
# 노드와 연결된 인접노드 탐색
for next_node, next_dist in graph[node].items():
distance = dist + next_dist # 인접노드까지의 거리
if distance < distances[next_node]: # 기존 거리 보다 짧으면 갱신
distances[next_node] = distance
heapq.heappush(queue, [distance, next_node]) # 다음 인접 거리를 계산 하기 위해 큐에 삽입
return distances효율적인 다익스트라 구현을 위해서 우선순위 큐를 사용합니다. 우선순위 큐는 거리의 최솟값(최단거리)부터 반환해주므로, 좀 더 빠르게 구할 수 있습니다. [ O( 간선의 개수 * log(노드의 개수) ) ]
2022.02.20 - [Algorithm] - [Algorithm] 힙(heap), 최소/최대로 정렬하는 우선순위 큐
[Algorithm] 힙(heap), 최소/최대로 정렬하는 우선순위 큐
그래프의 트리 구조 중 하나인 '힙'과 구현 방법에 대해 알아보고, 그와 관련된 우선순위 큐도 살펴보겠습니다. [ Contents ] 1. 완전 이진트리(Complete Binary Tree) 완전 이진트리: 왼쪽부터 오른쪽으
star7sss.tistory.com
# 입력
graph = {
'A': {'C': 1, 'D': 3},
'B': {},
'C': {'B': 2, 'D': 1},
'D': {}
}
print(dijkstra(graph, 'A'))
위에서 설명한 예제를 입력으로 넣어보면, 동일한 결과가 나옵니다.
3. 경로 추적
parents = {i: 0 for i in graph}최단거리 뿐만 아니라 '경로'도 역추적해서 찾을 수 있습니다. 우선 부모 노드(이전 노드)를 저장할 딕셔너리를 만듭니다. 맨 처음 각 자기 자신의 이전 노드는 없으니 0으로 설정합니다.
if distance < distances[next_node]: # 기존 거리 보다 짧으면 갱신
parents[next_node] = node # 이전 노드 저장최단거리를 갱신할 때마다, 어디서 왔는지 이전 노드를 기록합니다. B에서 C로 가는 경로로 갱신했다면, C의 이전 노드인 B를 저장합니다.
이렇게 이동할 때마다 '이전 노드'를 저장하면, 목적지에서 역으로 도착지를 추적할 수 있습니다.
path = []
curr = 'D'
while curr:
path.append(curr)
curr = parents[curr]
print(path[::-1])최단 경로를 역추적하기 위해, 목적지인 'D'의 이전 노드부터 찾습니다. 이후 반복해서 시작점인 'A'까지 찾고, 'A'의 이전 노드인 0(False)이 되면 반복이 종료됩니다. (맨 처음 초기화를 0으로 함)

path를 반대로 출력하면, 정상적으로 최단경로가 출력되는 걸 확인할 수 있습니다.
<최단경로 역추적까지 포함된 전체 코드>
import heapq # 우선순위 큐 구현을 위함
def dijkstra(graph, start):
distances = {node: int(1e9) for node in graph} # 처음 초기값은 무한대
distances[start] = 0 # 시작 노드까지의 거리는 0
queue = []
heapq.heappush(queue, [distances[start], start]) # 시작 노드부터 탐색 시작
while queue: # queue에 남아있는 노드가 없을 때까지 탐색
dist, node = heapq.heappop(queue) # 탐색할 노드, 거리
# 기존 최단거리보다 멀다면 무시
if distances[node] < dist:
continue
# 노드와 연결된 인접노드 탐색
for next_node, next_dist in graph[node].items():
distance = dist + next_dist # 인접노드까지의 거리
if distance < distances[next_node]: # 기존 거리 보다 짧으면 갱신
distances[next_node] = distance
parents[next_node] = node # 이전 노드 저장
heapq.heappush(queue, [distance, next_node]) # 다음 인접 거리를 계산 하기 위해 큐에 삽입
return distances
# 입력
graph = {
'A': {'C': 1, 'D': 3},
'B': {},
'C': {'B': 2, 'D': 1},
'D': {}
}
parents = {i: 0 for i in graph}
print(dijkstra(graph, 'A'))
path = []
curr = 'D'
while curr:
path.append(curr)
curr = parents[curr]
print(path[::-1])

'Algorithm' 카테고리의 다른 글
| [구현/수학] 백준 2167 2차원 배열의 합 - 파이썬(Python) (0) | 2022.03.23 |
|---|---|
| [자료구조/큐] 백준 18258 큐 2 - 파이썬(Python) (0) | 2022.03.22 |
| [탐색/백트래킹] 백준 9663 N-Queen - 파이썬(Python) (1) | 2022.03.21 |
| [수학/그리디] 백준 1049 기타줄 - 파이썬(Python) (0) | 2022.03.21 |
| [Algorithm] 백트래킹(Backtracking): 안될 싹은 미리미리 가지치기 (0) | 2022.03.20 |




댓글