[ Project ]
1. 프로젝트 개요
- 분류: 강화학습
- 일시: 2021.05. ~ 2021.06.
- 스택: OpenAI Gym, Pytorch, Python
- 주제: DQN, DDQN, Dueling DQN 강화학습 비교
GitHub - jangThang/Cartpole
Contribute to jangThang/Cartpole development by creating an account on GitHub.
github.com
2. 프로젝트 소개

Cartpole은 강화학습의 기본 예제입니다. 카트 위에 세워둔 막대기를 떨어뜨리지 않고, 카트를 움직이며 오랫동안 버텨야 합니다. Cartpole 강화학습 환경에서, 에이전트는 시행착오를 거치면서 노하우를 터득하게 됩니다.
Gym: A toolkit for developing and comparing reinforcement learning algorithms
Open source interface to reinforcement learning tasks. The gym library provides an easy-to-use suite of reinforcement learning tasks. import gym env = gym.make("CartPole-v1") observation = env.reset() for _ in range(1000): env.render() action = env.action_
gym.openai.com
해당 강화학습 환경은 OpenAI gym에서 다운로드 받으실 수 있으며, pip3을 이용해서 gym 라이브러리를 설치하셔도 됩니다.
| 학습종료까지 걸린 에피소드 | |
| DQN | 167 |
| DDQN | 191 |
| Dueling DQN | 114 |
해당 프로젝트는 Cartpole 강화학습 환경에서 DQN(Deep-Q-Network), DDQN(Double Deep-Q-Network), Dueling DQN(Duel Deep-Q-Network) 방식으로 각각 학습시킨 후 성능을 비교했습니다.
위 결과에 대한 해석은 3가지 강화학습 방식을 알아본 뒤, 후술하겠습니다.
● 프로젝트 목표
- OpenAI gym 강화학습 플랫폼을 사용해보고, 그 중 대표적인 'Cartpole' 환경을 분석 및 적용
- DQN, DDQN, Dueling DQN 구조 및 방법론에 대해 이론적으로 이해하고 적용
- DQN, DDQN, Dueling DQN 구조 및 방법론에 대한 장단저믈 살펴보고, 성능을 비교
3. 강화학습 환경 및 학습방법
1) Cartpole Environment

마찰이 없는 트랙 위, 검은색 카트(cart)에는 주황핵 폴(pole)가 하나 놓여져 있습니다. 폴과 카트의 연결부는 조작할 수 없으며, 오로지 카트(cart)만이 수평선을 따라 마찰없이 자유롭게 왔다갔다가 할 수 있습니다. 폴은 카트에 핀으로 연결돼 있는데, 이 핀을 축으로 자유롭게 회전할 수 있습니다.
에이전트는 이 카트에 왼쪽 혹은 오른쪽으로 일정한 힘을 가할 수 있습니다
● 목표: 막대기가 넘어지지 않도록 유지하며, 최대한 오래 유지하기
● 종료조건
- 막대기가 수직으로부터 12도 이상 기울어짐
- 카트가 중심으로부터 2.4 이상 벗어남
- 에피소드의 시간 스텝이 200보다 커짐
● 승리조건: 100번의 연속적인 시도에서 평균 195점 이상을 획득
● Observation
- X: 카트의 수평선 상의 위치
- X': 카트의 속도 폴이 수직선으로부터 기울어진 각도
- θ: 폴이 수직선으로부터 기울어진 각도
- θ': 폴의 각속도
| Observation | Min | Max | |
| X | Cart Position | -4.8 | 4.8 |
| X' | Cart Velocity | -Inf | Inf |
| θ | Pole Angle | -0.418rad (-24deg) | 0.418rad (24deg) |
| θ' | Pole Angular Velocity | -Inf | Inf |
● Action
- 왼쪽으로 카트 밀기
- 오른쪽으로 카트 밀기
(단, 속도가 감소하거나 증가하는 양은 pole의 θ에 따라 달라집니다. 카트와 폴이 이루는 각도에 따라 무게중심이 변하기 때문입니다.)
● 환경 속성
- Deterministic environment: 현재 상태에서 어떤 행동을 했을 때, 다음 상태가 확정
- Fully Observable environment: 강화학습을 진행하는 모든 시간동안, agent가 시스템의 상태를 관찰 가능
- Continuous environment: 실수 단위의 속도를 조정할 수 있어, 가능한 action의 수가 무한
- Episodic environment: 현재 action이 차후 episode의 action에 영향을 미치지 않으며 독립적
- Single agent environment: cartpole은 한 개로, 단일 agent로 구성된 환경
2) DQN

DQN방식은 Q function을 네트워크의 파라미터 θ로 근사하여 구하는 접근방식입니다.
Q(s, a;θ) ≈ Q^k(s, a) 근사하여 각 상태에서 가능한 모든 action의 Q-value를 계산합니다. Q-value를 계산하기위해서 Deep Q network를 구축하며, input layer는 구하고자하는 state가 입력되고 output layer는 해당 state에서 가능한 모든 action의 Q-value를 출력합니다. (input layer와 output layer는 FC layer로 구성합니다.)

정확한 Q value를 구하기 위해서, Deep Q Network도 파리미터를 학습하며 loss함수는 위와 같이 정의됩니다. Loss값은 Target value와 Predicted value의 차의 제곱형태로 나타냅니다.

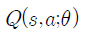
Target value를 구하는 네트워크와 predicted value를 구하는 네트워크가 동일하면, 둘 사이의 발산할 위험이 크기 때문에 별도 네트워크를 사용합니다. Target value의 Q value는 별도의 Target network를 사용하며, 특정 주기마다 실제 Q network의 가중치를 복사하여 업데이트합니다.
한편 Q network는 경사하강법(gradient descent)를 사용하여 최적해를 찾기 위해 가중치를 업데이트합니다.

DQN네트워크를 학습시키는 데이터는 Experience Replay에 저장된 데이터를 사용합니다. Cart-pole의 Transition을 그대로 네트워크에 학습하면, 시간축에 따른 correlation이 상당히 강하기 때문에 학습이 제대로 진행되지 않습니다. (특정 순간, 일련의 그러한 상황에서만 제대로 동작해서 일반화가 되지 않음)
따라서, 시간축에 따른 correlation을 줄이고자 Experience Replay에 transition 정보를 저장하고 랜덤으로 샘플링해서 학습에 사용합니다. Experience Replay는 Queue 자료구조와 유사하며, 버퍼가 가득차면 오래된 에피소드 정보를 지우고 최근의 에피소드 정보로 최신화합니다.
<전반적인 DQN 학습 과정>
1. Q-value를 구하고자하는 state를 DQN에 입력값으로 넣습니다.
(Cart-pole환경에서는 아타리게임환경과 같이 game screen을 state로 하지 않기 때문에 CNN과 같은 전처리 작업은 필요하지 않습니다.)
2. ε-greedy정책에 따라 action을 선택합니다. a = argmax(Q(s, a;θ))
3. action a를 선택한 뒤, 상태 s에서 수행하고 새로운 상태 s’로 transition된 reward를 받습니다.
4. 해당 transition을 replay buffer에 저장합니다. <s, a, r, s'>
5. replay buffer에서 임의의 transition 배치를 샘플링해서 loss를 계산합니다.
6. loss를 최소화하기 위해서 actual Q network의 파라미터에 대해서 경사하강법을 시행합니다.
7. 특정 주기마다, actual Q network의 파라미터를 target network의 파라미터에 복사합니다.
8. 이를 M개의 에피소드에 대해서 반복합니다.
3) DDQN
DQN방식은 Q-learning에서 max연산자를 사용해서 Q-value를 과대평가하는 경향이 있었습니다. 따라서 Q-value를 추정하는 과정에서 조금의 오차(noise)가 있으면 단순히 max연산자로 조금이라도 큰 것을 고르는 한계점이 있었습니다. (실제로는 다른 action이 최적)
이러한 문제를 해결하고자 DDQN에서는 각각의 독립적인 Q-function으로 추정합니다. 독립적인 두 Q-Function 중 하나는 action을 선택하고, 다른 하나는 action을 평가하여 좀 더 효과적으로 학습합니다.

즉, 다음 상태 S_t+1에서 Q-value가 최대가 되는 행동 a_m은 Actual Q-network에서 구하며, 그 때의 Q값은 Target Q-network에서 구합니다. DDQN은 Target network의 파라미터를 독립적으로 업데이트하고 action을 평가하므로 DQN의 한계점을 보완할 수 있었습니다.
4) Dueling DQN
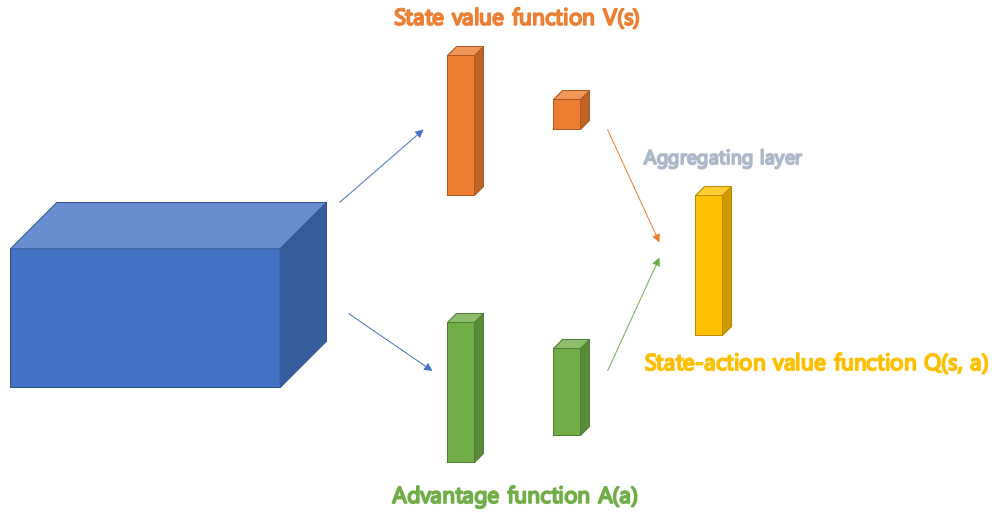
Double DQN은 네트워크를 독립적으로 2개를 구성해서 Actual Q network에서 최적의 action을 찾고, Target Q network에서 평가했었습니다. 반면 Dueling DQN은 Q-function을 state value function V(s)와 advantage function A(a)로 나누어서 구한다음, 합쳐서 Q-value를 구하는 방식입니다.

여기서 advantage function A(a)는 해당 state에서 가능한 action 중에서 해당 action이 얼마나 좋은지를 평가하며, Q(s,a)는 V(s)와의 합으로 구할 수 있습니다. (value function V(s)는 해당 state가 얼마나 좋은지 평가. 즉, 가능한 action들의 reward 평균으로 볼 수 있음)
Dueling DQN구조에서는 state value를 구하는 'value function stream'과 advantage value를 구하는 'advantage function stream'이 이중으로(Duel) 존재하며, 각각 목적에 맞게 특화되어 학습할 수 있다는 장점이 있습니다. 분업의 원리와 마찬가지로, 각각 V(s)와 A(a)를 구하여 합쳐 더 정확하고 효율적으로 Q(s,a)를 추정할 수 있습니다.
4. 프로젝트 결과
| 학습종료까지 걸린 에피소드 | |
| DQN | 167 |
| DDQN | 191 |
| Dueling DQN | 114 |
DQN에 비해, 별도 파라미터를 가지는 Target network를 구성하여 Q-value를 평가하고 학습하는 DDQN은 조금 더 학습하는 데에 시간이 필요했습니다. 반면, Value function stream과 Advantage function stream으로 각각 네트워크를 특화하여 학습하는 Dueling DQN은 114만에 학습을 완료했으며 DQN, DDQN보다 나은 성능을 확인할 수 있었습니다.

'Projects' 카테고리의 다른 글
| [Project] Patent Server: 특허 빅데이터 분석 플랫폼 (9) | 2022.03.24 |
|---|---|
| [Project] ST Fair Route: 모두가 공평한 네비게이션 앱 (0) | 2022.03.23 |
| [Project] Patent Big Data Analysis: 자연어 처리를 이용한 특허문서 분석 (1) | 2022.03.17 |
| [Project] SNUT RoadSign: SeoulTech 길찾기 프로그램 (0) | 2022.03.16 |
| [Project] Seoultech Explore: 모교 홍보를 위한 웹 게임(퀴즈) (0) | 2022.03.15 |




댓글